What’s in Store for 2010? A Few Predictions

“The only thing we know about the future is that it will be different.” – Peter Drucker

So let’s do some predictions, shall we? True, I dislike the entire business of prediction, close cousin that it is to guessing. Which I hate. But James’ excellent thoughts on what we might see in the year ahead got me thinking about what I’m anticipating.

Maybe we see over the hill imperfectly, but the following assertions are not without their substance either. Feel free to take them with a grain of salt, several grains, or not at all. We’ll see how we did a year from now.

One thing to keep in mind about our predictions: we’re looking a bit further out than, say, Gartner. Where they are predicting that cloud computing will a strategic technology for 2010, then, we instead consider that a given. So if you’re looking for predictions like, “open source will be a mainstream option,” you’ve come to the wrong place: we figure you know that already. It doesn’t mean that Gartner’s wrong, of course; merely that we’re having an entirely different conversation.

Cloud API Proliferation Will Become a Serious Problem

When I meet with cloud providers these days, the default answer to questions about the openness or lackthereof with respect to their software is “we have an open API.” But this is, unquestionably, the wrong answer for customers. It’s not that open APIs are bad, individually: far from it. You’d rather have one than not. But how are customers to manage them as they multiply? Cloud providers should be considering Kant’s Categorical Imperative:

“Act only according to that maxim whereby you can at the same time will that it should become a universal law.”

Unsurprisingly, however, they are not. Which means that cloud API proliferation will reach new, frightening heights in the year ahead. Or maybe you want to individually review and compare the APIs as they iterate. Watch the Deltacloud project for traction as a result; platforms with an API compatibility story like Eucalyptus should benefit as well.

On a semi-related note, I expect IaaS to remain more popular than PaaS for 2010.

Collaboration Will Never Be the Same

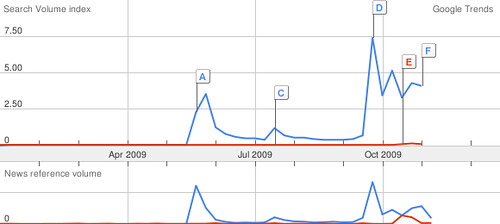
Google Wave was quite a splash when it landed; Mozilla Raindrop far less so. Or so says Google Trends. But both will play an important role in the fundamental reshaping of the interfaces – and in the case of Wave, infrastructure – that we all use to collaborate in the year ahead. Nor will the impacts be limited to the early adopter market those products are aimed at. As James noted, Lotus sold 1M licenses of its Connections product in two weeks to six customers. The appetite for next generation collaboration toolsets is strong, whether we’re talking about Rogers’ innovators or laggards.

But all of that may end up being the least interesting trend we see from collaboration in 2010. Of potentially greater impact are those that go beyond the interface. Github, for example, strongly incents social coding and cross pollination in ways that change the way development is done. Offerings like Gist and Threadsy, meanwhile, take a business intelligence-like approach to email, attempting to both consolidate multiple streams and process the content algorithmically according to its inter-relation. Message from your boss? Important. Someone you hear from once every two months? Less so. Neither are ready for primetime, by my testing, but they point the way forward.

And collaboration will never be the same.

Data as Revenue

I’ve written about this fairly extensively already, so I won’t belabor the point. But we’re going to see datasets increasingly recognized as a serious, balance sheet-worthy asset. Twitter pointed the way with its Bing and Google deals, and then Infochimps reinforced that value by making available, commercially, data they harvested from everyone’s favorite micro-blogging service.

This will continue. I’m fully in agreement with IBM’s Steve Mills when he says that we’re “moving into an era of information led transformation.” As margins slim and economies continue to stagnate, enterprises of all sizes will increasingly turn their eyes to data based assets, both for their latent commercial value as well as for improved decision making.

As a result, fear and concern over the privacy implications will spike.

Democratization of Big Data

Yes, Facebook and its 24 terabytes of new content per day is an outlier. But what about the individual developer that wants to make sense of the 1.7 GB Twitter dataset that Infochimps is making available? OpenOffice.org, as I can personally report, doesn’t want anything to do with it.

Fortunately, the democratization of big data is well underway. Hadoop puts MapReduce within reach, Pig puts Hadoop within reach, and with the Cloudera desktop you even have a nice, shiny browser based GUI. Throw in Amazon, and you have as many machines as you could possibly want. We’re still a little light in the front end space, with the ability to visualize the data lagging far behind the ability to process it, but that will come. Maybe in the next year, maybe not.

But either way, the ability to work on big data will increasingly be available to any business, large or small. Democractization of Big Data, commence.

Developer Target Fragmentation Will Accelerate

Between cloud fabrics, programming language proliferation, mobile application development and the spike in development framework popularity, development targets have been fragmenting for several years now. We are more or less in full retreat from the one time promise of write once, run anywhere as an industry. I see nothing on the horizon that will throttle or even slow this trend; if anything, the increasing volume of cloud platforms and the surge in interest in mobile development will accelerate this trend.

This has significant implications for purveyors of middleware, application development tools and cloud platforms, but also for those charged with setting enterprise technology standards. The CIO’s job is going to get harder in 2010, because picking a winner from the myriad language, framework and platform options will be much more difficult than picking a safe option.

It’s All About the Analytics

Flowing Data, a blog run by PhD candidate Nathan Yau, is one of my favorites. The visualization of data is as much an art as a science, and there are few practitioners more talented. The challenge of taking data and hammering it into a form that conveys meaning and supports conclusions is, of course, an age old challenge. But the tools at our disposal are getting better, fast.

Consider the simple analytics that are available, for free, to virtually anyone today: Google Analytics for the web, Feedburner for feeds, Bit.ly for links, About:Me for the browser, Flickr Stats for pictures and so on. Emerging services like PostRank will even extend that value by consolidating various streams into a meaningful, single glance assessment of performance.

I’ve never subscribed to the idea that only what can be measured can be managed – open source, in particular, belies that claim – but there’s no debate that metrics can be immensely important in maximizing returns, and to an extent, profits.

We’re going to see analytics become, as James said, ubiquitous to the extent that they’re not already. Two projects to keep your eyes on in this space, both from IBM: the chronically underleveraged ManyEyes, and the Hadoop-backed M2. Both could – should, in my view – be important at advancing the state of analytics forward in the next year.

Marketplaces Will Be Table Stakes

Why has it taken so long for the idea of marketplaces to catch on? Don’t look at me; I’ve been banging on about them since 2006 or so. The equation has long seemed like a no brainer to me: developers and ISVs get a centralized channel and wider audience, platforms get a wider ecosystem, and customers get a more efficient discovery and acquisition process – at a minimum.

Whatever the initial reluctance, that’s over. Two plus billion Apple iTunes store downloads later, mobile players are falling all over themselves to roll out marketplaces to compete. Canonical, sponsors of the Ubuntu project, are moving towards their own software store (though, regrettably, it still doesn’t include developers as I’ve hoped for). Amazon, meanwhile, has most of the pieces it would need to sell apps, and a sustained rate of innovation that is more or less unmatched in the industry at present.

What does 2010 hold, then? Marketplaces, and a lot of them. Mobile is quickly becoming staturated, web apps and the desktop are probably next, and data marketplaces may ultimately eclipse them all. If you want to play next year, bring your marketplace. Or go home.

New Languages to Watch

Seems like we have a new hot programming language every year. Some are in it for the long haul, some fade away, and some linger in between like the undead. I’m not prepared at this point to call the winners for the next year, but two that a.) might lend themselves well to cloud and cloud-like environments and b.) are receiving disproportionately more attention relative to their erstwhile competition are Clojure and Go. The former is essentially Lisp reborn on top of the JVM, while Go borrows from C syntaticly but adds in modern language conveniences such as garbage collection without taking too much of a hit performance-wise (Go is 20-30% slower than C/C++, reportedly).

It seems unlikely that either will make significant inroads at the expense of the currently popular compiled languages such as C#/Java or the dynamic alternatives (PHP/Python/etc), but the level of attention – and the people paying attention – distinguish them from other languages aimed at concurrency like Erlang and Haskell.

NoSQL Will Bid for Mainstream Acceptance

Maybe the NoSQL label is a misnomer, and maybe Michael Stonebraker is right that NoSQL has nothing to do with SQL. Either way, I am not ready to predict that the NoSQL moniker will retired in favor of, say, AltDB.

What I will claim, however, is that projects in this space will individually and collectively make serious bids for mainstream acceptance. Cassandra, CouchDB, InfiniDB, MongoDB, Riak, Tokyo Cabinet and the like – different as they all are from one another – will position themselves not as relational replacements but complementary technologies that solve a different set of problems.

While I don’t believe the bid for mainstream acceptance will be successful generally – enterprises are too wedded to the RDBMS model, the tooling for the NoSQL projects is generally weak, etc – they will find a fertile ground in areas illsuited to the traditional relational, row-based model.

So that’s my nine. As a bonus, five predictions for free and open source software:

FOSS Predictions

1. Usage of dual licensing will continue to decline, in part because of the Oracle and EU dispute over MySQL
2. FOSS advocates will increasingly turn their attention from licensing to the related mechanisms of copyright and trademark
3. Permissive licensing will continue to gain at the expense of reciprocal licensing, albeit slowly
4. The value of project code will be eclipsed, in a few cases, by the data the project generates
5. Open source, building from its mainstream acceptance, will emerge as the most credible alternative to proprietary cloud and mobile platforms

But that’s just what I’m seeing. What are your predictions for 2010?

Update: Nat Torkington’s done an excellent follow up that looks at the opportunity side of the above: highly recommend you go read it.

Disclosure: Basho (Riak), Canonical, Cloudera, IBM, Oracle, Sun (MySQL) are RedMonk customers. Apple, Google and Mozilla are not.

Related posts:

1. links for 2010-03-04
2. Three Predictions: Languages, Databases, and Collaboration
3. links for 2010-01-22
4. links for 2010-01-12
5. Who’s Going to Build the App Store for the Enterprise?